L. de Menezes and Wolfgang J.R. Hoefer
In most practical cases, the solution of electromagnetic problems has to rely on the use of numerical methods. Some of these techniques use the approximation of differential operators by difference ones. This represents the substitution of the continuous problem by the discrete one. In all consistent numerical methods, the solution of the difference equations tends to the differential counterpart as the discretization step tends to zero.
However, the discrete solution can converge slower to the continuous one in the vicinity of discontinuities. The reason is the finite number of modes propagating in the mesh that represents the continuous space. Moreover, the propagation constant of each of these modes can differ considerably from the continuous counterparts,. The overall effect is a reduction of the accuracy of the representation of modes near discontinuities.
Some of these effects cannot be predicted by the dispersion analysis of the difference equation, which expresses the relationship between modes and frequency warping of the solutions. This work advances further in this direction by solving analytically the difference equation of the numerical scheme, subjected to the actual boundary conditions of the problem. The closed-form solution can be only obtained in certain cases, which allows some conclusions about the propagation behavior of the modes present in a general case.
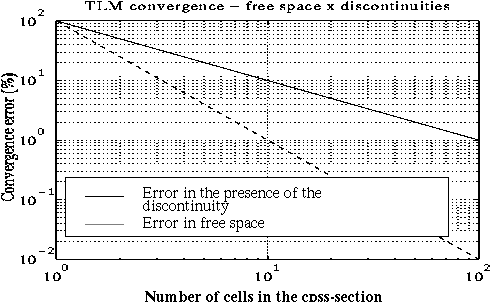
In this work, the analytical solution of the two dimensional shunt node TLM method is obtained for the special case of a capacitive diaphragm in a TEM waveguide. The solution provides the behavior of the susceptance of the discrete structure, which is compared to the actual continuous solution. It is shown that the accuracy of the field is reduced from second to first order with the introduction of the discontinuity.

Fig.1 Convergence of the susceptance on the capacitive diaphragm